Ingrid Cloud's score sheet
For turbulence sound
Background
This NASA/AIAA benchmark presents a direct comparison of simulation results obtained using Ingrid Cloud’s intelligent algorithm with wind tunnel measurements on a Gulfstream G550 nose landing gear Figure 1 The objective was to assess the accuracy of Ingrid Cloud’s solver when predicting turbulent flow and noise generation by the landing gear of an aircraft approaching landing. The experimental work was carried out by researchers from the NASA Langley Research Center [1] and provided a series of detailed, well-documented wind tunnel measurements for comparison and validation of simulation results.
The surface mesh in Figure 1 clearly illustrates how we create the “initial guess” volume mesh. On the one hand, the surface of the landing gear is accurately represented in its finest details. On the other hand, the mesh is dramatically coarser close to wind tunnel walls, away from the landing gear (with cell sizes that are as large as the wheels themselves). This way, we leave the decision of where to refine the volume mesh to Ingrid Cloud’s intelligent algorithm, which will then produce a fine mesh based on the choice of output. In this problem, the output chosen was the turbulent sound generated by the landing gear.

Surface mesh (left) and “initial guess” volume mesh (right). For the computations, we fed the “initial guess” volume mesh into Ingrid Cloud’s intelligent algorithm so that it could perform automatic mesh refinement and compute sound sources originated when an aircraft approaches landing.
Method
This problem was solved in a one way, uncoupled system of equations, where incompressible Navier-Stokes equations were solved to compute the flow and a wave propagation problem was solved to compute sound. Both equations are complemented by their continuous adjoint equations and their solutions are used, together with other heuristics, to compute error estimations and refine the mesh.
For this benchmark, the refinement goal was the sound sources of Lighthill’s wave equation [2]. Both fluid and sound problems were solved simultaneously on the same mesh to avoid I/O and interpolation issues; the supercomputer “Beskow” at PDC Center for High Performance Computing in Stockholm was used.
Results
Below Figure 2 shows the volume mesh for different levels of refinement. The finest mesh is clearly more refined in the wake of the gear (the flow is from left to right) and refinement is performed so that the flow structures important for computation of sound are correctly resolved, leaving other areas unrefined.



Volume mesh refined by Ingrid Cloud from “initial guess” (left) to final mesh (right). The adaptive algorithm is an iterative process where several iterations are performed before the final mesh is obtained. Here, only 3 iterations are shown for simplicity.
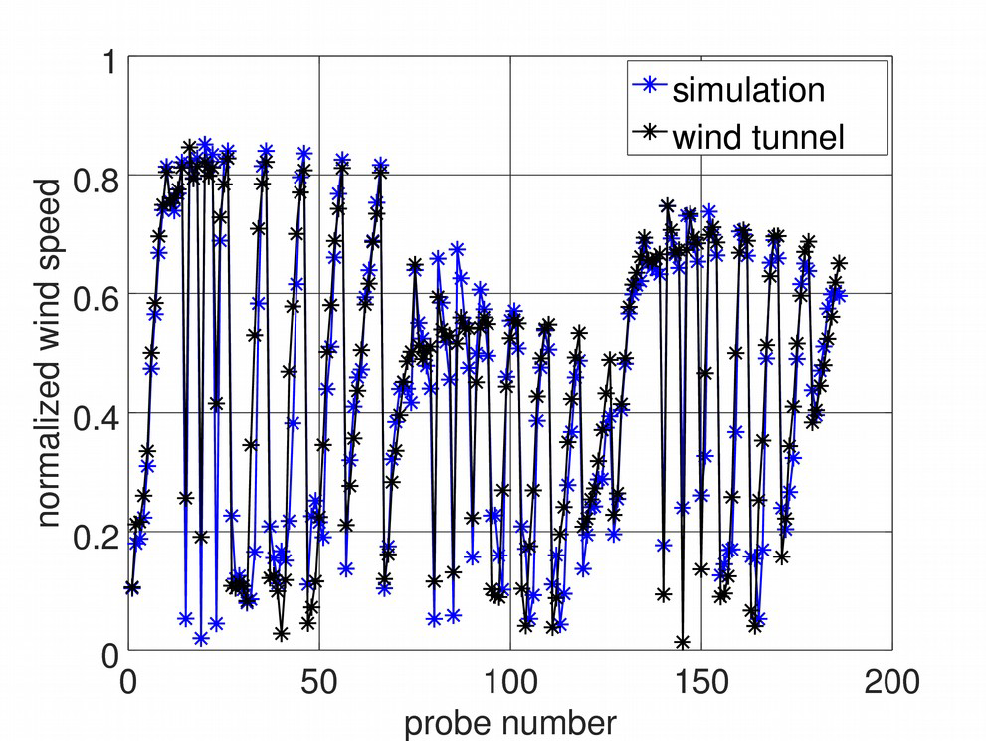
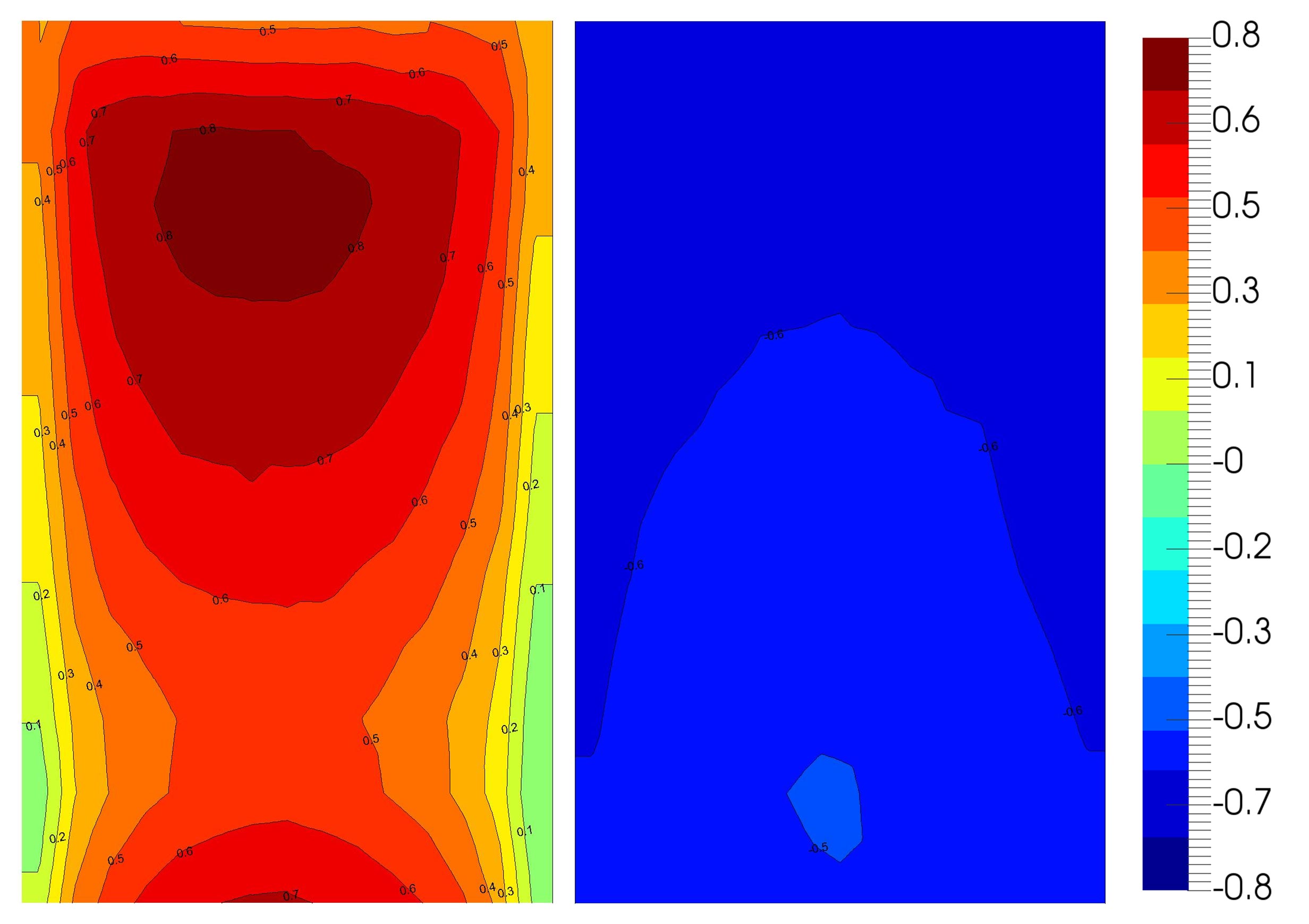
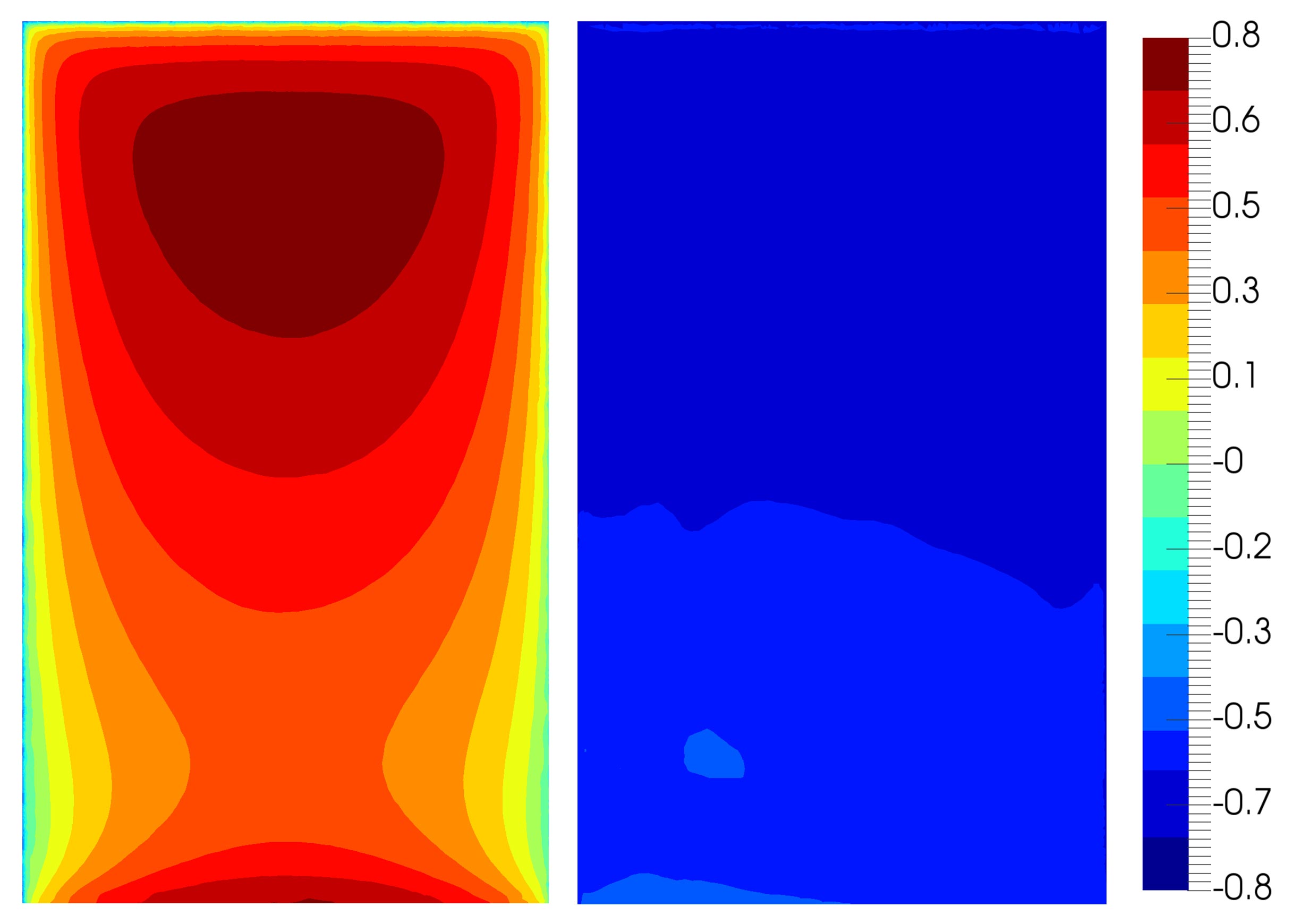
Below Figure 3 brings an overview comparison with wind tunnel PIV plane measurements, where time-averaged contours of streamwise velocity, 2D turbulent kinetic energy (TKE) and Z-vorticity are shown; the quantities were plotted on two planes, one passing through the starboard wheel and the other through the wake of the landing gear door.
There is a good qualitative agreement between experiments and simulation. One remarkable feature of the comparison is that there is a clear asymmetry between the port and starboard sides when observing the door plane, both in the streamwise velocity and TKE fields. This is not an intuitive result; however, a closer look at the geometry reveals that the landing gear is indeed asymmetrical with respect to its longitudinal plane. The adaptive mesh refinement automatically captures this behaviour, which would be a somewhat intricate task had we generated and refined the mesh manually.
Another interesting feature of the comparison is that we apparently get an overshoot of vorticity on the side of the starboard wheel; this is probably due to the low resolution of the PIV measurement as compared to the resolution of the computational mesh, and not an “overshoot”: the wheels constitute a strong source of unsteadiness and we expect the mesh refinement to capture this behaviour, producing a fine mesh in that area. The PIV resolution is 1.3 mm [1] and the computational mesh close to the wheels is smaller than 1.3 mm on several cells coinciding with the region of strongest vorticity.

PIV, location of measurement planes; time-averaged fields of streamwise velocity, 2D turbulent kinetic energy and vorticity. In all figures: left, simulation, right, measurements [11].
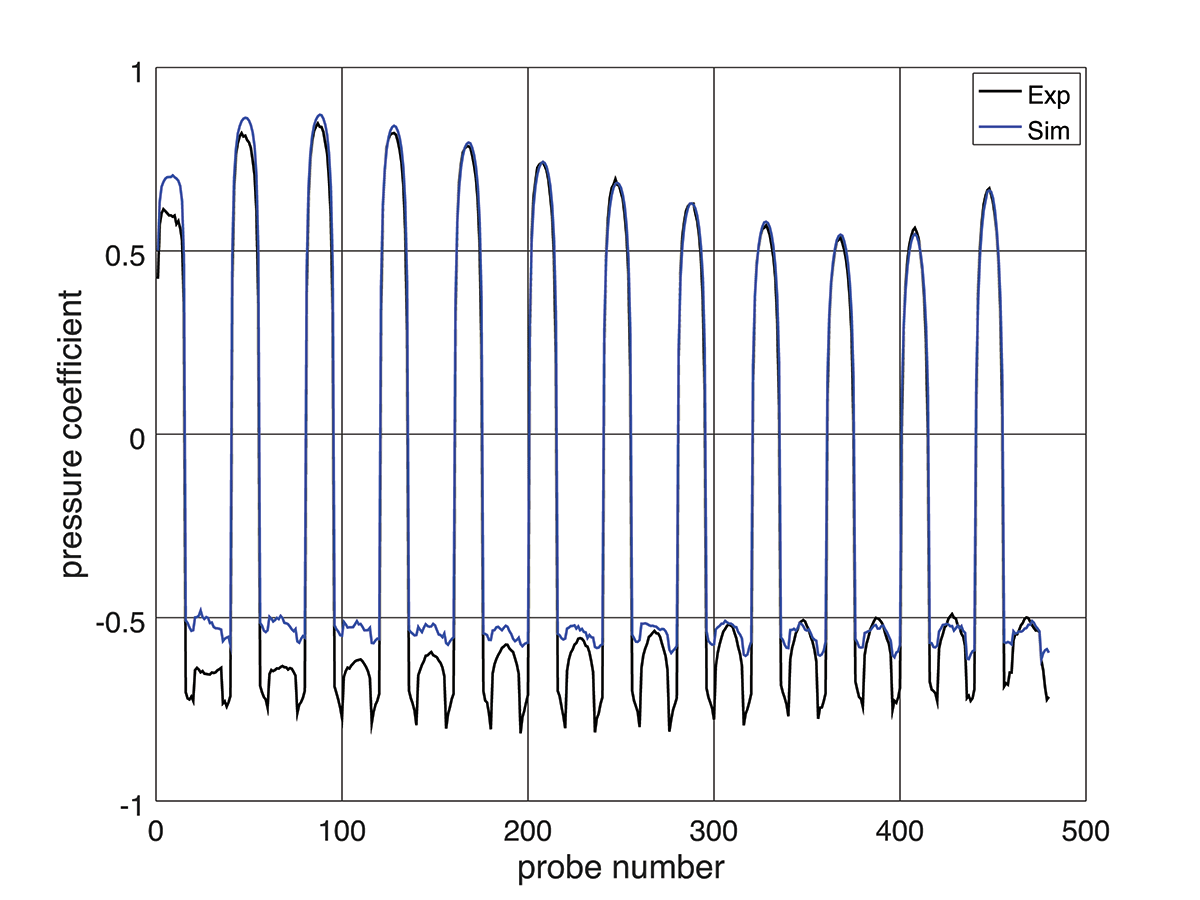
Sound pressure levels were measured at 20 different locations at the University of Florida Aeroacoustic Flow Facility (UFAFF), Figure 4. A selection of 6 representative microphones is compared with measured values in Figure 5. The signals compare well, especially in the frequency range of 800–2000 Hz for the flyover microphones, and 1000–9000 Hz for the sideline ones. The sideline microphones show, in general, better agreement, which may be a consequence of lack of resolution in the mesh, causing dispersion of waves as they travel a longer distance (flyover microphones are ca. 1 m further away from the gear than sideline ones).

Microphone locations in the UFAFF wind tunnel.
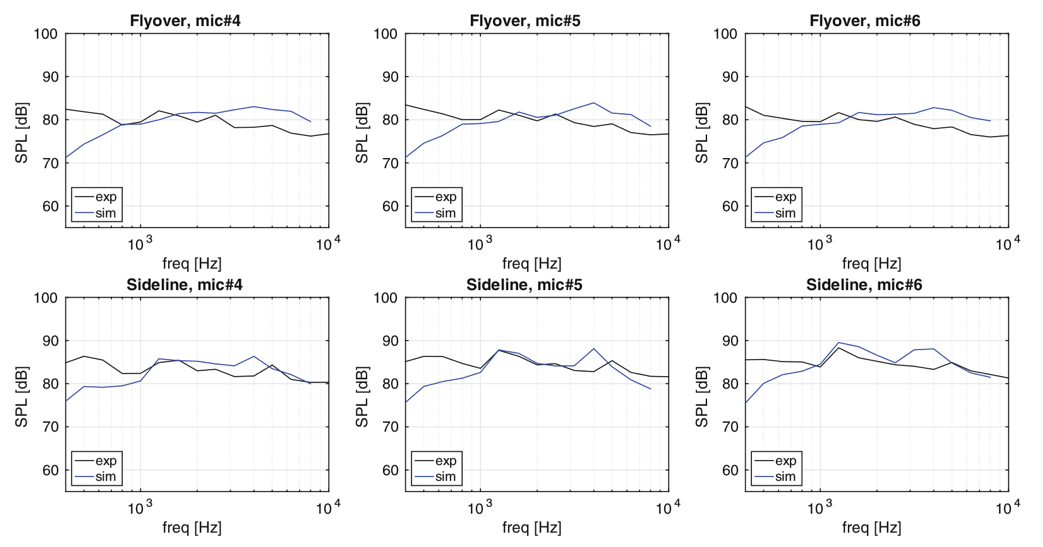
Comparison of Sound Pressure Level (SPL) for selected microphones.
Finally, Figure 6 shows a comparison of the integrated error of the sound pressure levels in all microphones between Ingrid Cloud’s computations and the computations performed by a direct competitor. Thanks to its intelligent algorithms, Ingrid Cloud largely outperforms the competitor’s computations.
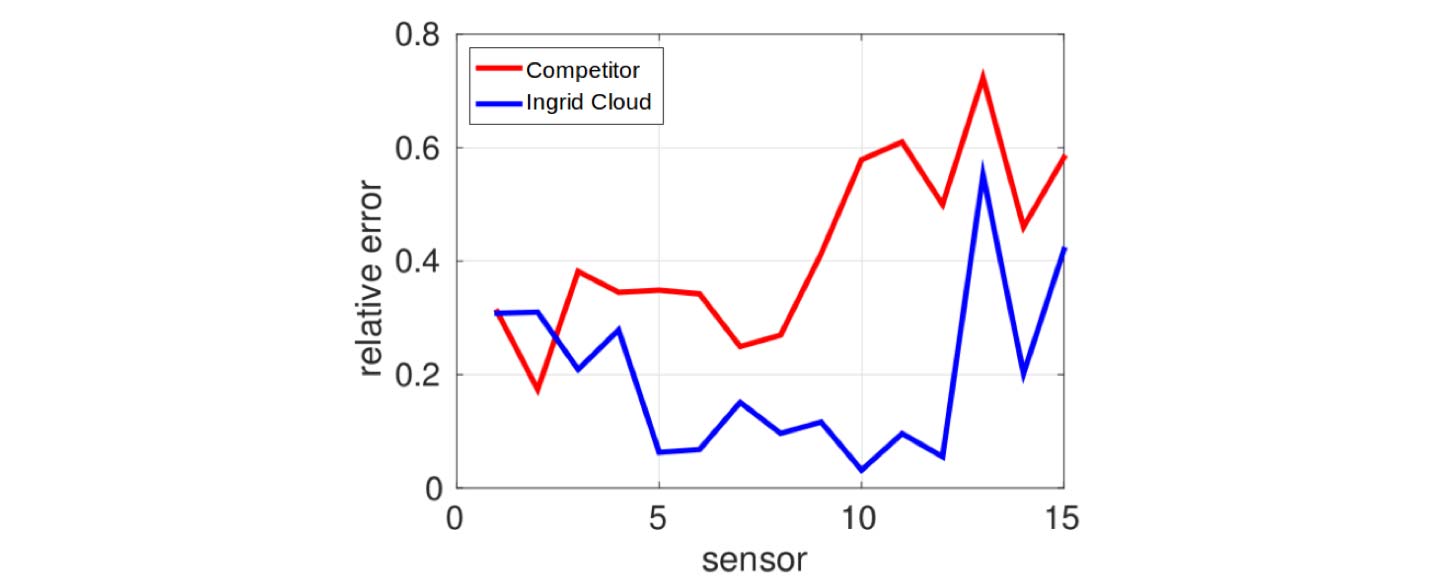
Comparison of integrated error in all microphones, showing that Ingrid Cloud outperforms a major competitor.
References
[1] Neuhart DH et al (2009), Aerodynamics of a gulfstream g550 nose landing gear model, In Proceedings for the 15th AIAA/CEAS Aeroacoustics Conference (30th AIAA Aeroacoustics Conference).
[2] Vilela de Abreu R et al (2011), Adaptive computation of aeroacoustic sources for a rudimentary landing gear using Lighthill’s analogy, In Proceedings for the 17th AIAA/CEAS Aeroacoustics Conference (32nd AIAA Aeroacoustics Conference).